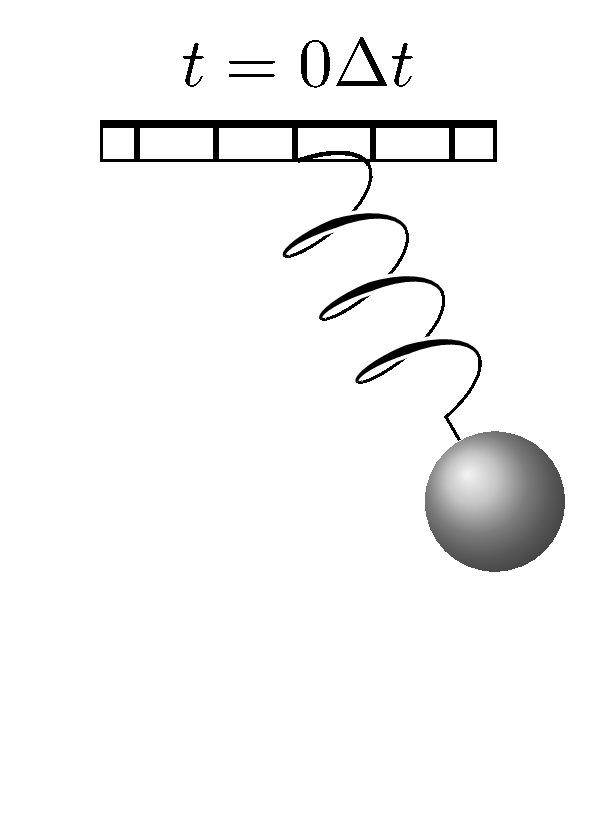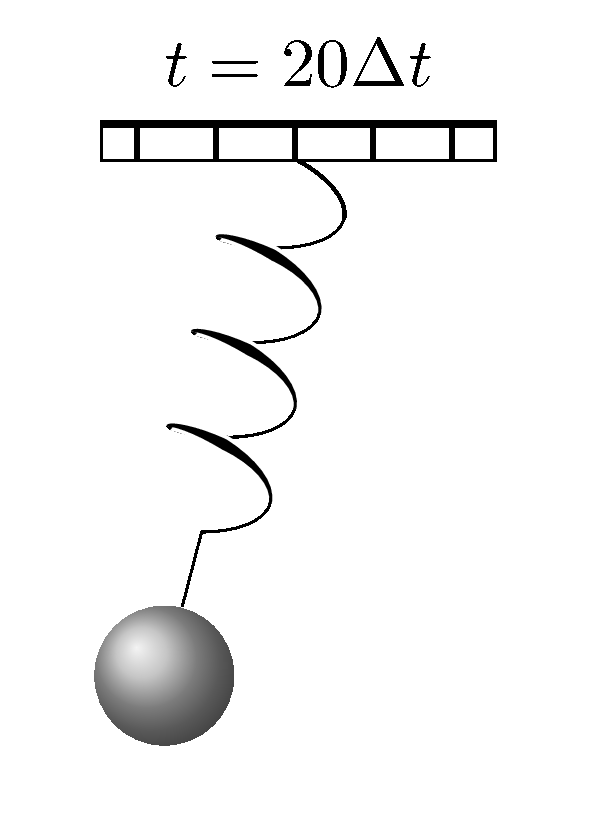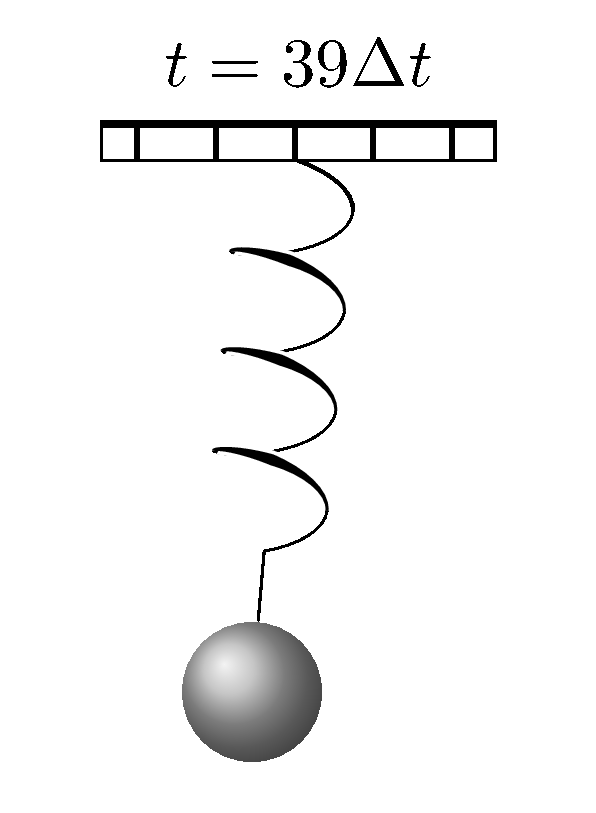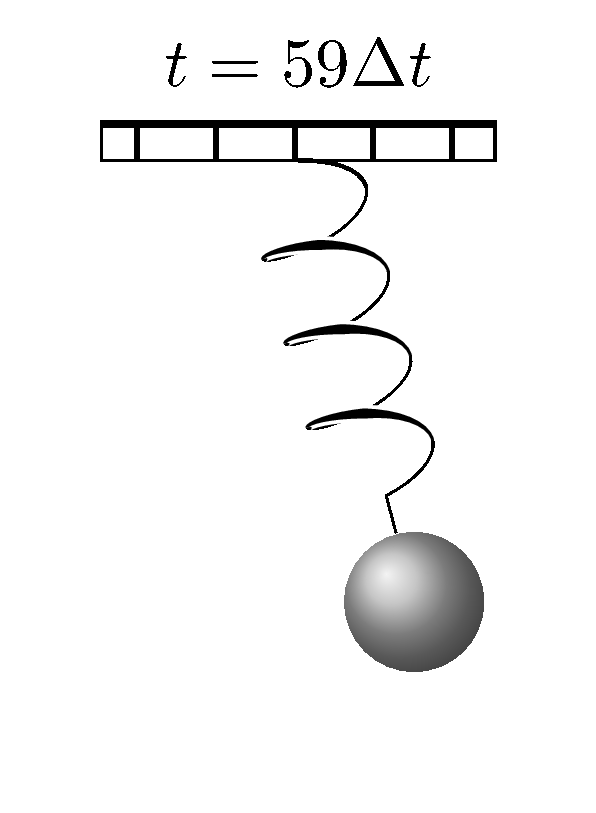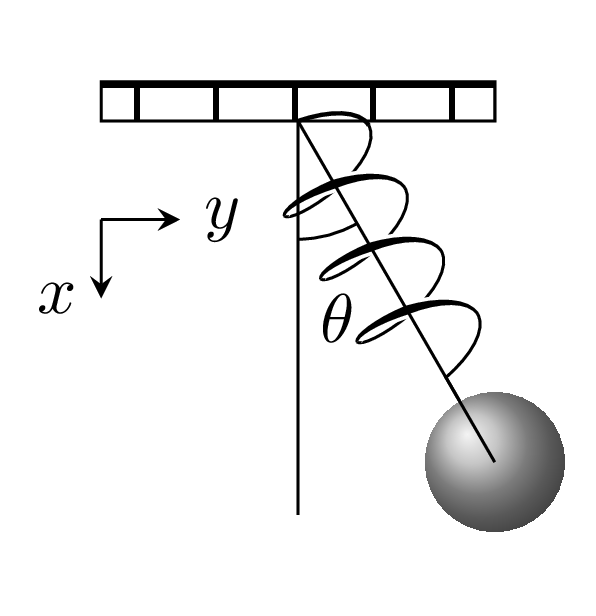
When we analysed a tilted oscillator that we transformed the equations of motion from Cartesian coordinates to polar coordinates. The same can be done here for a simple pendulum with a harmonic potential, except that the angle $\theta$ is not a constant anymore. \begin{align} \frac{dr}{dt}&=\omega_r\\ \frac{d\theta}{dt}&=\omega_{\theta}\\ \frac{d\omega_r}{dt}&=r\omega_{\theta}^2-\frac{k}{m}(r-L)+g\cos\theta\\ \frac{d\omega_{\theta}}{dt}&=-\frac{2}{r}\omega_{\theta}\omega_{r}-\frac{g}{r}\sin\theta \end{align} This results in a system of nonlinear differential equations. And the equations make sense in a way that the force due to the harmonic potential is going to affect the value of $r(t)$ only, but not the angle. It can be solved numerically using Newton's method once the equations are discretized and the Jacobian matrix is known. Such numerical method has been discussed when we evaluated the upper limit of the age of the Moon. An animation was created using the numerical solutions to the above system of nonlinear differential equations.