
It is well-known that as the Earth spins, a misalignment of tidal bulges is created, which leads to two unequal forces acting on the Moon along the tangential direction of the orbit. These two unequal forces ($F_n$ and $F_f$) are in opposite direction and the difference in their magnitudes is as follows: $$ F_n-F_f\approx 6rGmy\Big(\frac{m_b}{R^4}\Big) $$ $r$ is the Earth's radius, $y$ is the misalignment distance of the tidal bulge, $R$ is the distance between the centers of the Earth and the Moon, $G$ is the gravitational constant, $m$ is the mass of the Moon and $m_b$ is the mass of the tidal bulge. It is known that $m_b$ is proportional to $R^{-3}$ that $m_b=C_1R^{-3}$. The above equation can be now rewritten as: $$ F_n-F_f\approx 6rGmy\Big(\frac{C_1}{R^7}\Big) $$ With the fact that the velocity of any object ($V$), which is the Moon in this case, in the circular orbit can be expressed as: $$ V=\sqrt{\frac{G(M+m)}{R}} $$ $M$ is the mass of the Earth. Differentiation of $V$ with respect to time $t$ gives us: $$ \frac{dV}{dt}=\frac{-\sqrt{G(M+m)}}{2R^{3/2}}\frac{dR}{dt} $$ With Newton's law of motion, we get: $$ \frac{dR}{dt}=\frac{-2R^{3/2}}{\sqrt{G(M+m)}}\cdot 6rGy\Big(\frac{C_1}{R^7}\Big) $$ $y$ is proportional to the difference between Earth's spinning rate ($\omega$) and the angular velocity of the Moon ($\omega_L$) that $y=C_2(\omega-\omega_L)$.
This leads to the following first order ODE:
$$ \frac{dR}{dt}=CR^{-5.5}(\omega-\omega_L) $$ With $C$ replacing all the product of constants. As we would like to integrate this from present time to the time in the past, we apply the coordinate transformation ($t=t_1-t'$, where $t_1$ is present time), such that we can easily solve this equation using implicit Euler's method. $$ \frac{dR}{dt'}=-CR^{-5.5}(\omega-\omega_L) $$ With initial condition: $$ R(t'=0)=384400~\mathrm{km} $$ $\omega$ and $\omega_L$ are the spin rate of Earth and the angular velocity of the Moon, respectively, which can be derived using Kepler's third law and law of conservation of angular momentum and are expressed as follows: $$ \omega=\frac{L}{p}-\frac{Mm}{p}\sqrt{\frac{G}{M+m}}\cdot\sqrt{R} $$ $$ \omega_L=\sqrt{G(M+m)}\cdot R^{-1.5} $$ $L$ is the angular momentum of Earth-Moon system, $p$ is the polar moment of Earth's inertia. With $a=\sqrt{G(M+m)}$ and $b=\frac{Mm}{p}\sqrt{\frac{G}{M+m}}$, as well as implicit Euler's method: $$ R_{i+1}=R_i-\Big[CR_{i+1}^{-5.5}(\frac{L}{p}-b\sqrt{R_{i+1}}-aR_{i+1}^{-1.5})\Big]\Delta t' $$ The objective function for internal iteration with Newton's method is defined as: $$ g=R_{i+1}-R_i+\Big[CR_{i+1}^{-5.5}(\frac{L}{p}-b\sqrt{R_{i+1}}-aR_{i+1}^{-1.5})\Big]\Delta t' $$ $$ \frac{\partial g}{\partial R_{i+1}}=1+\Big(\frac{-5.5CL}{p}R_{i+1}^{-6.5}+5CbR_{i+1}^{-6}+7aCR_{i+1}^{-8}\Big)\Delta t' $$ In Newton's method, the value of $R_{i+1}^{(k)}$ at the $k$th iteration is updated using the following formula: $$ R_{i+1}^{(k+1)}=R_{i+1}^{(k)}-\Big(\frac{g}{\frac{\partial g}{\partial R_{i+1}}}\Big)^{(k)} $$ Due to the stability of implicit Euler's method, we can use a large $\Delta t'=1000~\mathrm{years}$.

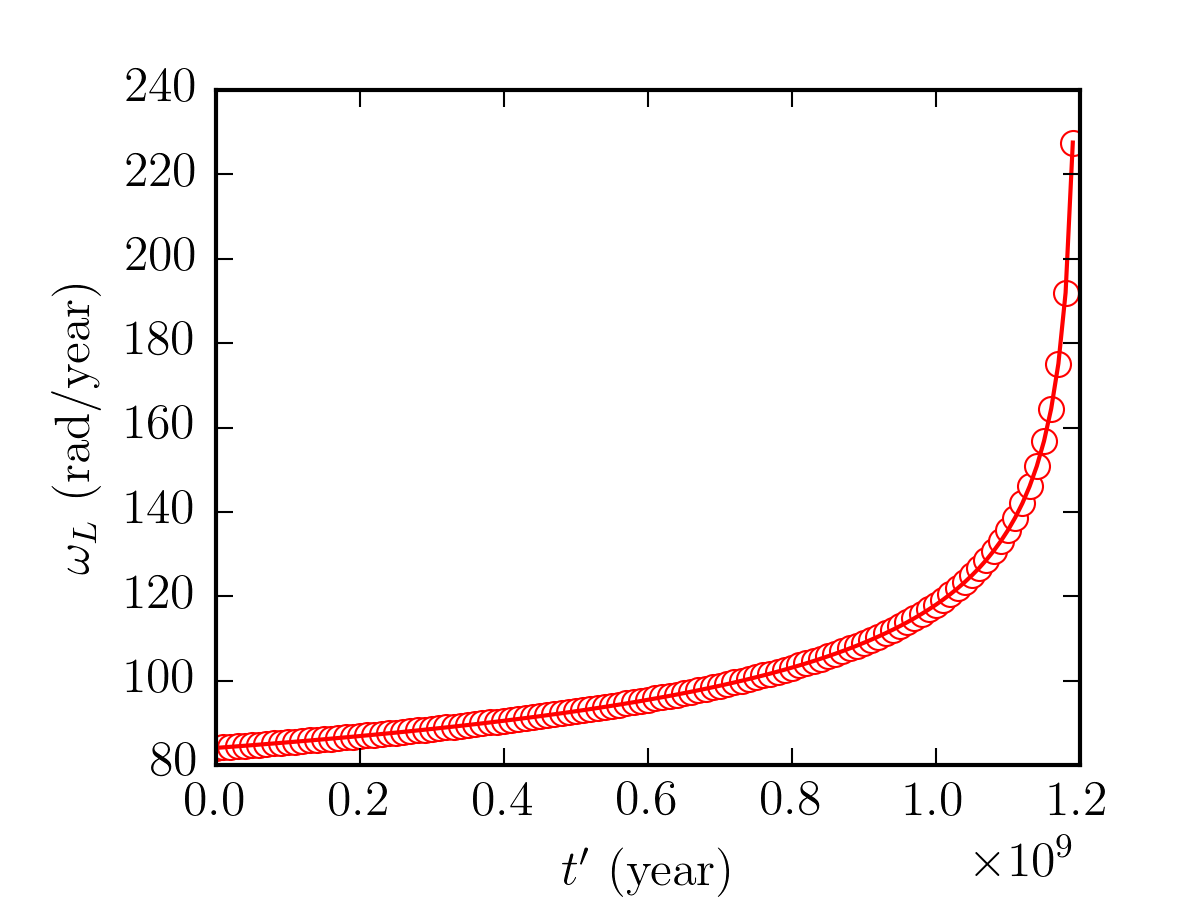
As shown in Figures 1 and 2, the upper limit of the Moon's age is approximately $1.2\cdot 10^{9}$ years.