Consider the situation that a particle is subjected to a stochastic force and a harmonic potential. The continuity equation can be written as:
\begin{align*}
\frac{\partial c}{\partial t}=D\vec{\nabla}_r^2c+\vec{\nabla}_{\vec{r}}\cdot k_s\zeta^{-1}\vec{r}c
\end{align*}
$\vec{v}=-k_s\zeta^{-1}\vec{r}$, and $\zeta$ is the friction coefficient. The following operator $\Gamma$ can be defined as:
\begin{equation}
\Gamma=D\vec{\nabla}_{\vec{r}}^2+\vec{\nabla}_{\vec{r}}\cdot k_s\zeta^{-1}\vec{r}
\end{equation}
The Green function $G(\vec{r},\vec{r}',t)$ is defined as the probability for particle to be at $\vec{r}$ at $t=0$ and at $\vec{r}'$ at time $t$. Hence, an average property such as $\langle r^2(t)\rangle$ can be defined as:
\begin{equation}\label{eq:2}
\langle r^2(t)\rangle = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty} d\vec{r}d\vec{r}'r'^2G(\vec{r},\vec{r}',t)\Phi_{eq}(\vec{r})
\end{equation}
$\Phi_{eq}(\vec{r})$ is the equilibrium distribution of vector $\vec{r}$. From Equation (\ref{eq:2}), if we take derivative with respect to time:
\begin{equation}
\frac{\partial}{\partial t}\langle r^2(t)\rangle=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty} d\vec{r}d\vec{r}'r'^2\Gamma G(\vec{r},\vec{r}',t)\Phi_{eq}(\vec{r})
\end{equation}
This is because $\frac{\partial}{\partial t}G=\Gamma G$. It can be figured out that by integration by parts:
\begin{equation}
\frac{\partial}{\partial t}\langle r^2(t)\rangle=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty} d\vec{r}d\vec{r}'(D\vec{\nabla}^2_{\vec{r}'}-k_s\zeta^{-1}\vec{r}'\cdot\vec{\nabla}_{\vec{r}'})(r'^2) G(\vec{r},\vec{r}',t)\Phi_{eq}(\vec{r})
\end{equation}
Let us evaluate the following:
\begin{equation}
\vec{\nabla}_{\vec{r}'}^2(r'^2)=6
\end{equation}
And
\begin{equation}
\vec{r}'\cdot\vec{\nabla}_{\vec{r}'}r'^2=2r'^2
\end{equation}
The equation can thus be further simplified as:
\begin{equation}
\frac{\partial}{\partial t}\langle r^2(t)\rangle = 6D-2k_s\zeta^{-1}\langle r^2(t)\rangle
\end{equation}
which gives us the solution:
\begin{equation}
\boxed{\langle r^2(t)\rangle=\langle r^2(0)\rangle\exp(-2k_s\zeta^{-1}t)+\frac{6D\zeta}{2k_s}[1-\exp(-2k_s\zeta^{-1}t)]}
\end{equation}
Similarly, we can define for the vector correlation function:
\begin{equation}
\langle \vec{r}(t)\cdot\vec{r}(0)\rangle=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}d\vec{r}d\vec{r}'\vec{r}\cdot\vec{r}'G(\vec{r},\vec{r}',t)\Phi_{eq}(\vec{r})
\end{equation}
\begin{equation}
\frac{\partial}{\partial t}\langle\vec{r}(t)\cdot\vec{r}(0)\rangle=-\frac{k_s}{\zeta}\langle\vec{r}(t)\cdot\vec{r}(0)\rangle
\end{equation}
This is because we have:
\begin{equation}
\vec{r}'\cdot\vec{\nabla}_{\vec{r}'}\vec{r}'=\vec{r}'
\end{equation}
Therefore:
\begin{equation}
\langle \vec{r}(t)\cdot\vec{r}(0)\rangle=\langle r^2(0)\rangle\exp\Big(-\frac{k_s}{\zeta}t\Big)
\end{equation}
The mean-square displacement:
\begin{equation}
\boxed{\langle[\vec{r}(t)-\vec{r}(0)]^2\rangle=\langle r^2(t)\rangle-2\langle \vec{r}(t)\cdot\vec{r}(0)\rangle+\langle r^2(0)\rangle}
\end{equation}
Putting all these together, we then have:
\begin{align*}
\boxed{\langle[\vec{r}(t)-\vec{r}(0)]^2\rangle=\langle r^2(0)\rangle\exp(-2k_s\zeta^{-1}t)+\frac{6D\zeta}{2k_s}\cdot[1-\exp(-2k_s\zeta^{-1}t)]-2\langle r^2(0)\rangle\exp(-\frac{k_s}{\zeta}t)+\langle r^2(0)\rangle}
\end{align*}
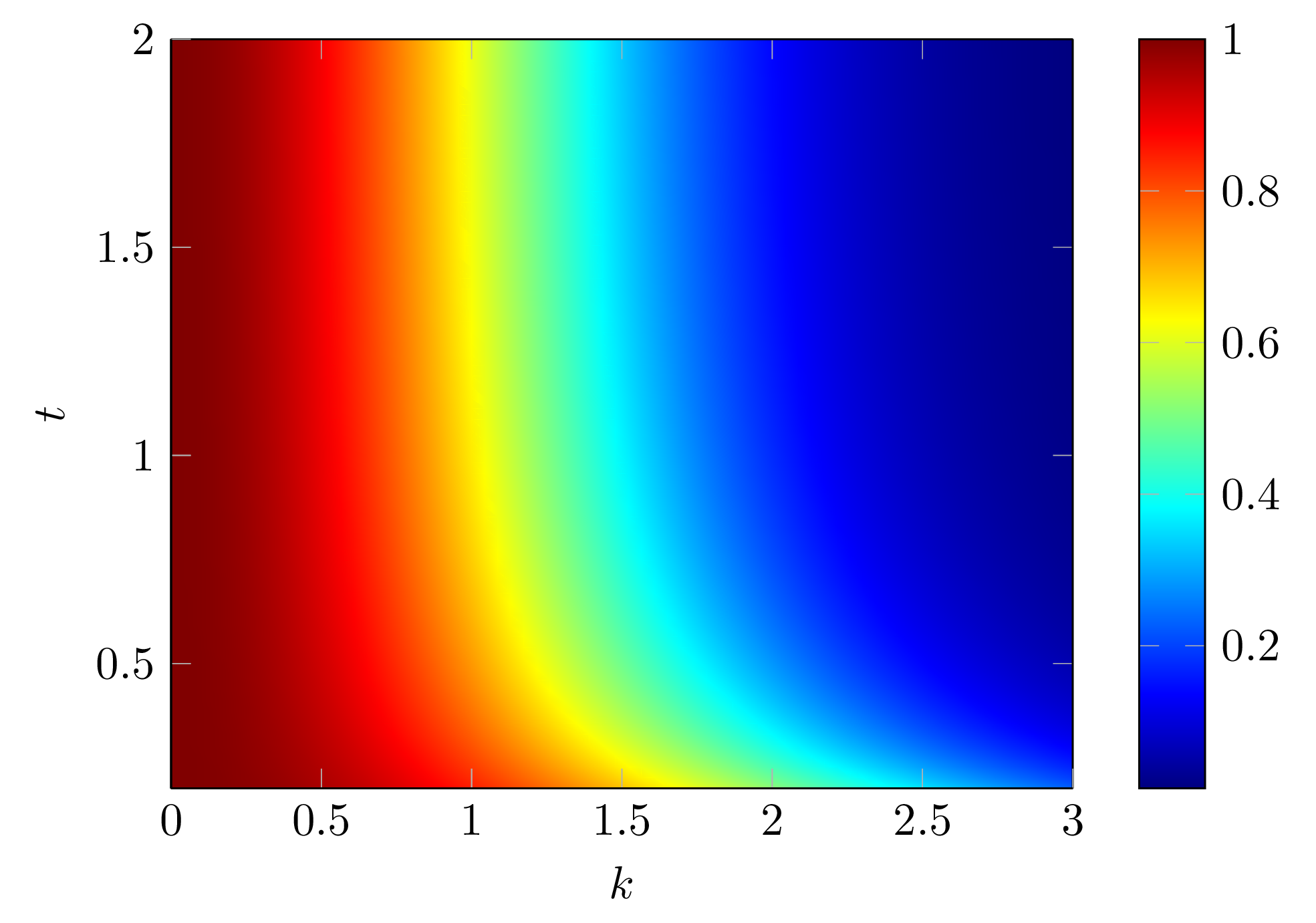
The dynamic light scattering function will then be:
\begin{equation}
g(k,t)=\exp(-\frac{k^2}{6}\langle [\vec{r}(t)-\vec{r}(0)]^2\rangle)
\end{equation}
With $\langle r^2(0)\rangle$ being zero, we can plot $g(k,t)$ straightforwardedly.