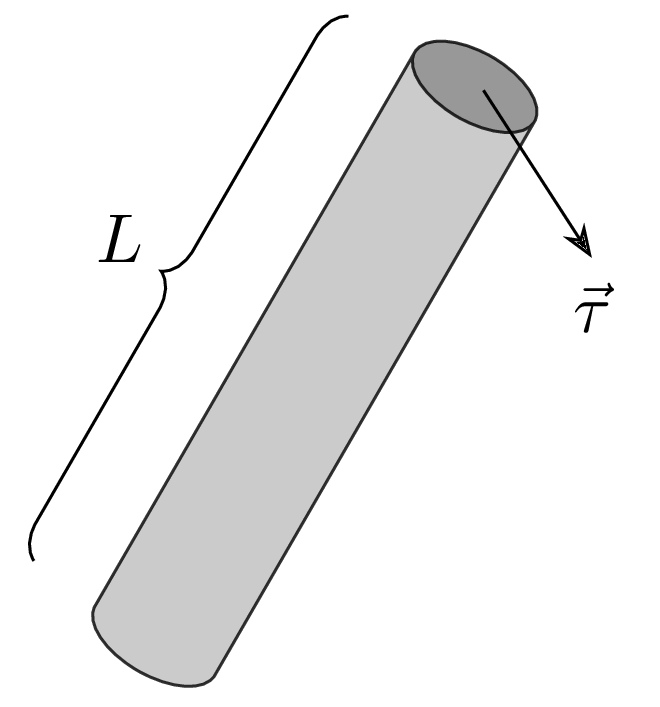
Again, introducting the Green function, which is now a function of the orientation of the rigid rod: \begin{align} \frac{\partial G(\hat{r},\hat{r'},t)}{\partial t}&=D\vec{\nabla}_{\vec{r}}^2G(\hat{r},\hat{r'},t) \end{align} where $\hat{r}=\begin{bmatrix}\cos\psi\sin\theta \\ \sin\psi\sin\theta \\ \cos\theta\end{bmatrix}$. The operator $\vec{\nabla}_{\vec{r}}^2$ should be written in spherical coordinate, as we are now interested in the rotational diffusion of the rod.
\begin{align*} \vec{\nabla}^2_{\vec{r}}= \frac{1}{L^2\sin\theta}\frac{\partial}{\partial \theta}\sin\theta\frac{\partial}{\partial \theta}+ \frac{1}{L^2\sin^2\theta}\frac{\partial^2}{\partial\psi^2} \end{align*} In the rotational motion, the length $L$ does not change. Consider the property of the vector correlation function $\langle \hat{r}(t)\cdot\hat{r}(0)\rangle=\langle \cos\theta(t)\rangle$: \begin{equation} \langle \cos\theta(t)\rangle=\int d\hat{r}\int d\hat{r}'\cos\theta G(\hat{r},\hat{r'},t)\Phi_{eq}(\hat{r}') \end{equation} \begin{equation} \frac{\partial}{\partial t}\langle \cos\theta(t)\rangle=\int d\hat{r}\int d\hat{r}' (D\vec{\nabla}^2_{\vec{r}}\cos\theta)G(\hat{r},\hat{r'},t)\Phi_{eq}(\hat{r}') \end{equation} \begin{equation} \frac{\partial}{\partial t}\langle \cos\theta(t)\rangle=-\frac{2D}{L^2}\langle \cos\theta(t)\rangle \end{equation} \begin{equation} \boxed{\langle \hat{r}(t)\cdot\hat{r}(0)\rangle=\exp\Big(-\frac{2D}{L^2}t\Big)} \end{equation} This is useful as we calculate the zero-shear viscosity of the rigid rods.