Diffusion equation with convection term is written as follows:
\begin{equation}
\frac{\partial}{\partial t}c=D\vec{\nabla}^2c-\vec{v}\cdot\vec{\nabla}c
\end{equation}
Multiply both sides by a factor of $e^{\vec{a}\cdot\vec{r}}$, on the right hand side, we thus have:
\begin{align}
&De^{\vec{a}\cdot\vec{r}}\vec{\nabla}^2c-e^{\vec{a}\cdot\vec{r}}\vec{v}\cdot\vec{\nabla}c\\
&=D\vec{\nabla}^2e^{\vec{a}\cdot\vec{r}}c-2D\vec{a}e^{\vec{a}\cdot\vec{r}}\cdot \vec{\nabla}c-Da^2e^{\vec{a}\cdot\vec{r}}c-e^{\vec{a}\cdot\vec{r}}\vec{v}\cdot\vec{\nabla}c
\end{align}
It can be deduced that:
\begin{align}
\boxed{\vec{a}=-\frac{\vec{v}}{2D}}
\end{align}
As $C=e^{-\frac{\vec{v}}{2D}\cdot\vec{r}}c$, the equation then becomes:
\begin{equation}
\boxed{\frac{\partial C}{\partial t}=D\vec{\nabla}^2C-\frac{v^2}{4D}C}
\end{equation}
\begin{align*}
\hat{C}(k,t)=\hat{C}(k,0)\exp\Big(-k^2Dt-\frac{v^2}{4D}t\Big)
\end{align*}
This means that:
\begin{equation}
C(r,t)=\frac{1}{8\pi^{1.5}(Dt)^{1.5}}\exp\Big(-\frac{v^2}{4D}t\Big)\exp\Big(-\frac{r^2}{4Dt}\Big)
\end{equation}
\begin{equation}
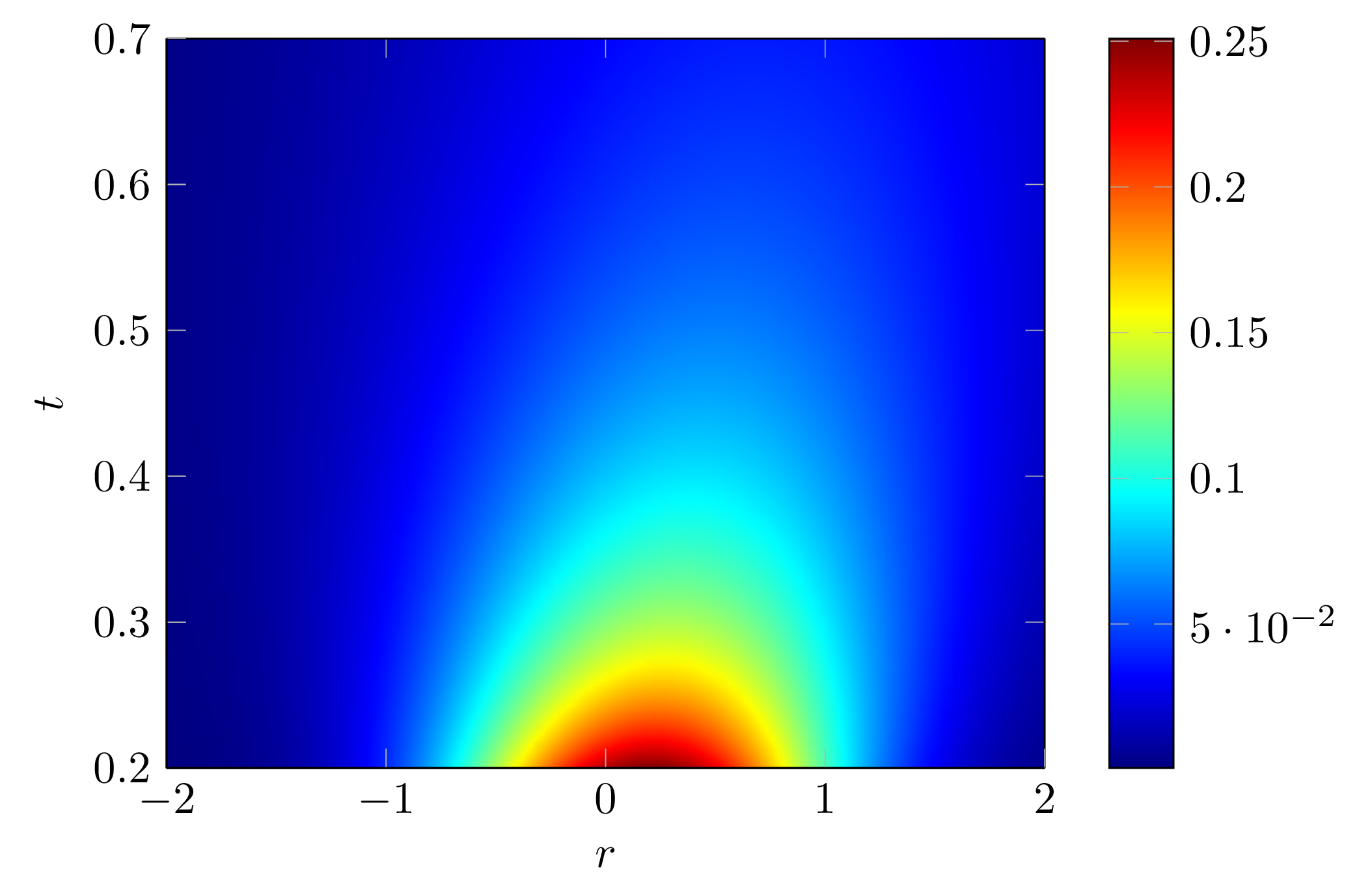
\boxed{c(r,t)=\frac{1}{8\pi^{1.5}(Dt)^{1.5}}\exp\Big(-\frac{v^2}{4D}t\Big)\exp\Big(-\frac{r^2}{4Dt}+\frac{\vec{v}\cdot\vec{r}}{2D}\Big)}
\end{equation}