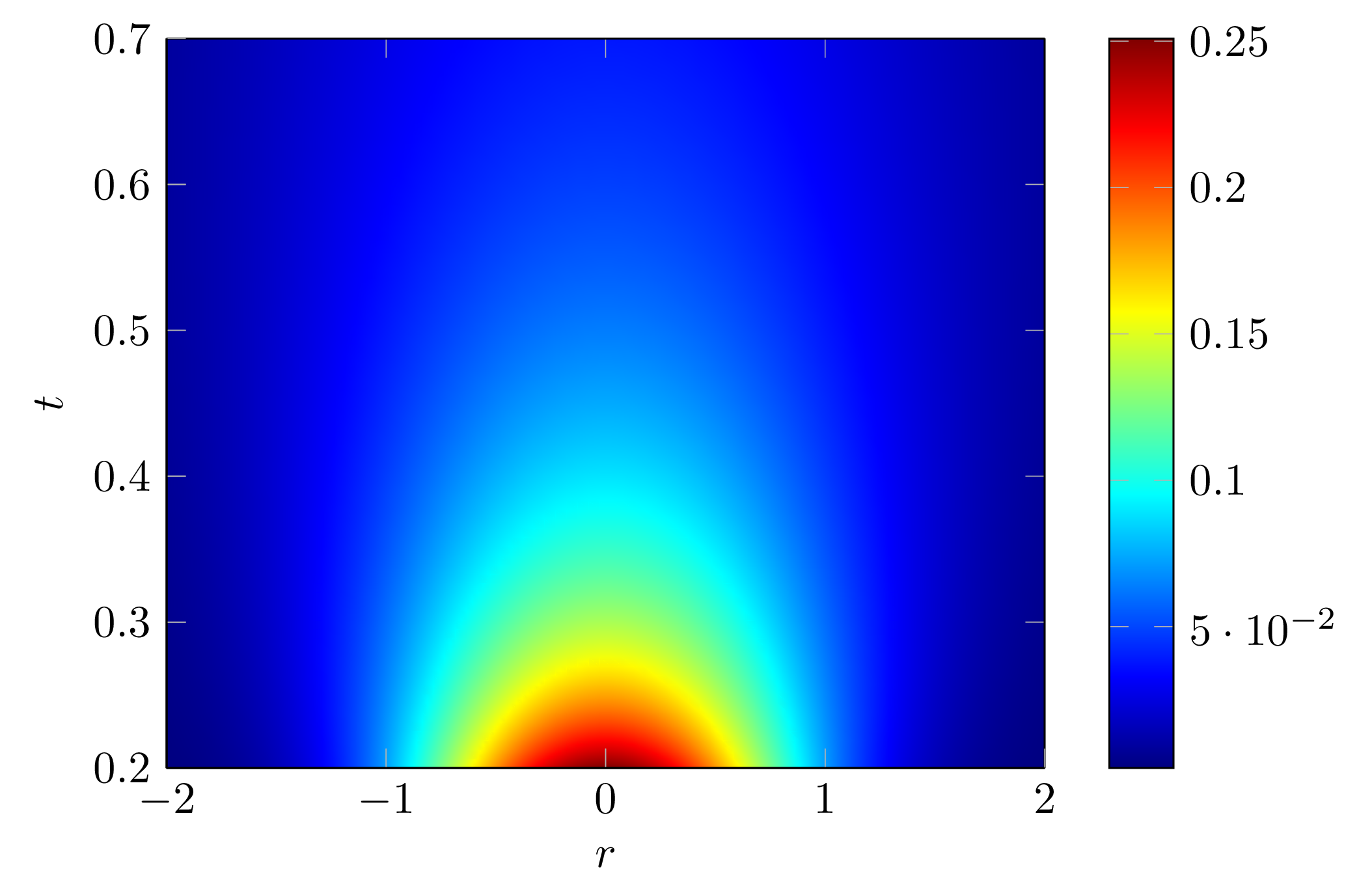
By the conservation of mass, continuity equation for non-uniform fluid with a number density of $c(\vec{r},t)$ can be written as: \begin{equation} \frac{\partial}{\partial t}c(\vec{r},t)=-\vec{\nabla}_{\vec{r}}\cdot c(\vec{r},t)\vec{v} \end{equation} A diffusive flux vector $\vec{j}=-D\vec{\nabla}_{\vec{r}} c$, where $D$ is the diffusion coefficient: \begin{equation} \frac{\partial}{\partial t}c = D\vec{\nabla}_{\vec{r}}^2c \end{equation} This can be solved using Fourier Transformation: \begin{equation} \hat{c}(\vec{k})=\int_{-\infty}^{\infty}e^{-i\vec{k}\cdot\vec{r}}c(\vec{r})d\vec{r} \end{equation} \begin{equation} c(\vec{r})=\frac{1}{8\pi^3}\int_{-\infty}^{\infty}e^{i\vec{k}\cdot\vec{r}}\hat{c}(\vec{k})d\vec{k} \end{equation} The R.H.S. of the diffusion equation is as follows: \begin{align} &\int_{-\infty}^{\infty}e^{-i\vec{k}\cdot\vec{r}}D\vec{\nabla}_{\vec{r}}^2 c(\vec{r})d\vec{r} \end{align} By integration by parts: \begin{align} &=i\vec{k}\cdot\int_{-\infty}^{\infty} D\vec{\nabla}_{\vec{r}} c(\vec{r})e^{-i\vec{k}\cdot\vec{r}}d\vec{r} \end{align} Again by integration by parts: \begin{align} &=-k^2\int_{-\infty}^{\infty}e^{-i\vec{k}\cdot\vec{r}}c(\vec{r})d\vec{r}=-k^2\hat{c}(\vec{k}) \end{align} \begin{align} \boxed{\hat{c}(\vec{k},t)=\hat{c}(\vec{k},0)e^{-k^2Dt}} \end{align} With the inital value $\hat{c}(\vec{k},0)=1$, we can transform $\hat{c}(\vec{k},t)$ back to the real space: \begin{align} c(\vec{r},t)=\frac{1}{2\pi^2}\int_0^{\infty}\frac{\sin kr}{kr}e^{-k^2Dt}k^2dk \end{align} $\frac{\sin(kr)}{kr}$ can be broken down into two terms using Euler formula: \begin{align} c(\vec{r},t)&=\frac{1}{2\pi^2}\int_0^{\infty}\Big[\frac{e^{ikr}-e^{-ikr}}{2ikr}\Big]e^{-k^2Dt}k^2dk\\ c(\vec{r},t)&=\frac{1}{4i\pi^2r}\int_0^{\infty}[e^{-k^2Dt+ikr}-e^{-k^2Dt-ikr}]kdk \end{align} \begin{align} \boxed{c(\vec{r},t)=\frac{e^{-\frac{r^2}{4Dt}}}{4i\pi^2r}\Big(\frac{ir\sqrt{\pi}}{2Dt\sqrt{Dt}}\Big)=\frac{1}{8\pi^{1.5}(Dt)^{1.5}}\exp\Big(-\frac{r^2}{4Dt}\Big)} \end{align}