As we have a MD trajectory of multiple coarse-grained benzene rings in a box, we can calculate the van hove function and extract the diffusion coefficient of the system.

Again, with the MD trajectory, the van hove function can easily be generated with the following command:

Similar to the case of PEO chains, in the file van_hove.xvg, the van hove function $G(r,t)$ is expressed in the real space. It can be easily transformed to the fourier space, using the following: \begin{equation} \hat{G}(k,t)=4\pi\int_0^{\infty}\frac{\sin(kr)}{kr}G(r,t)r^2dr \end{equation}

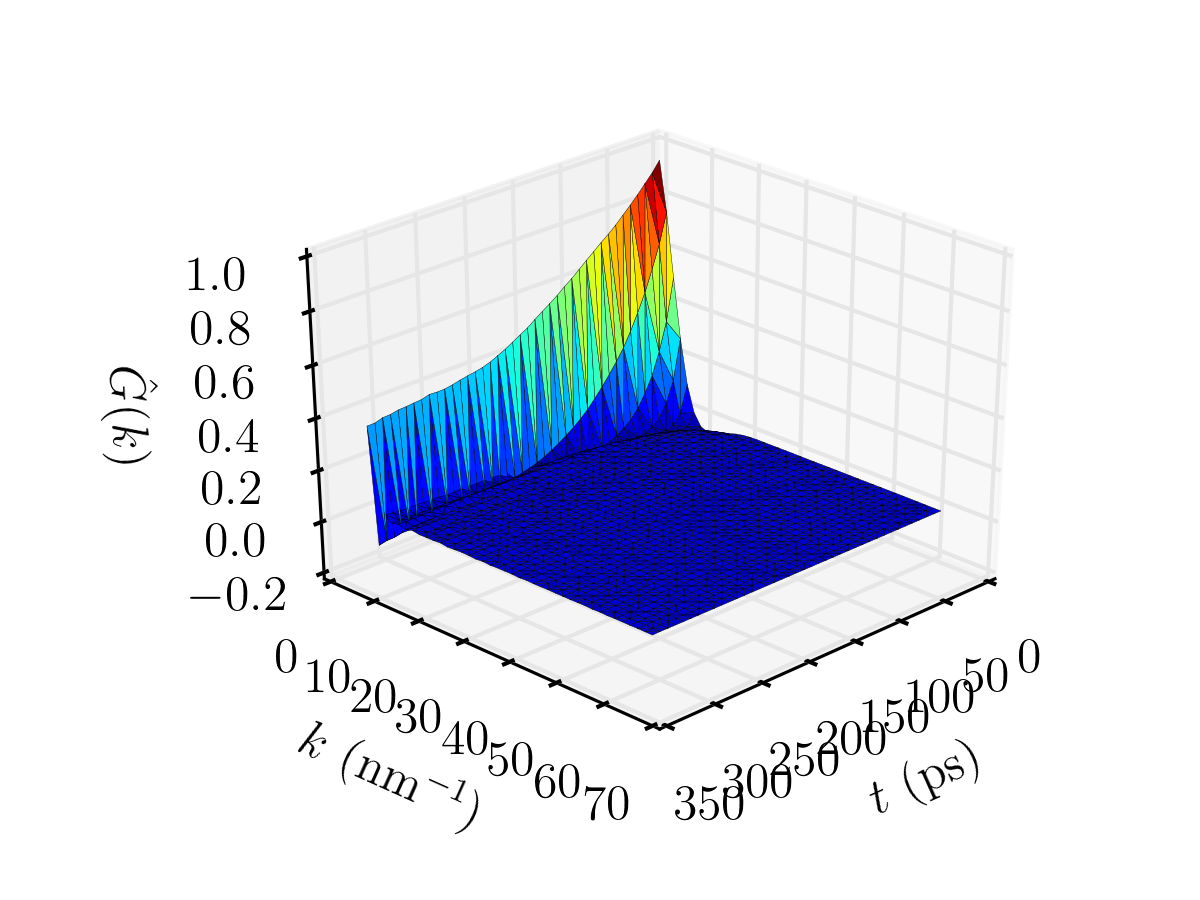
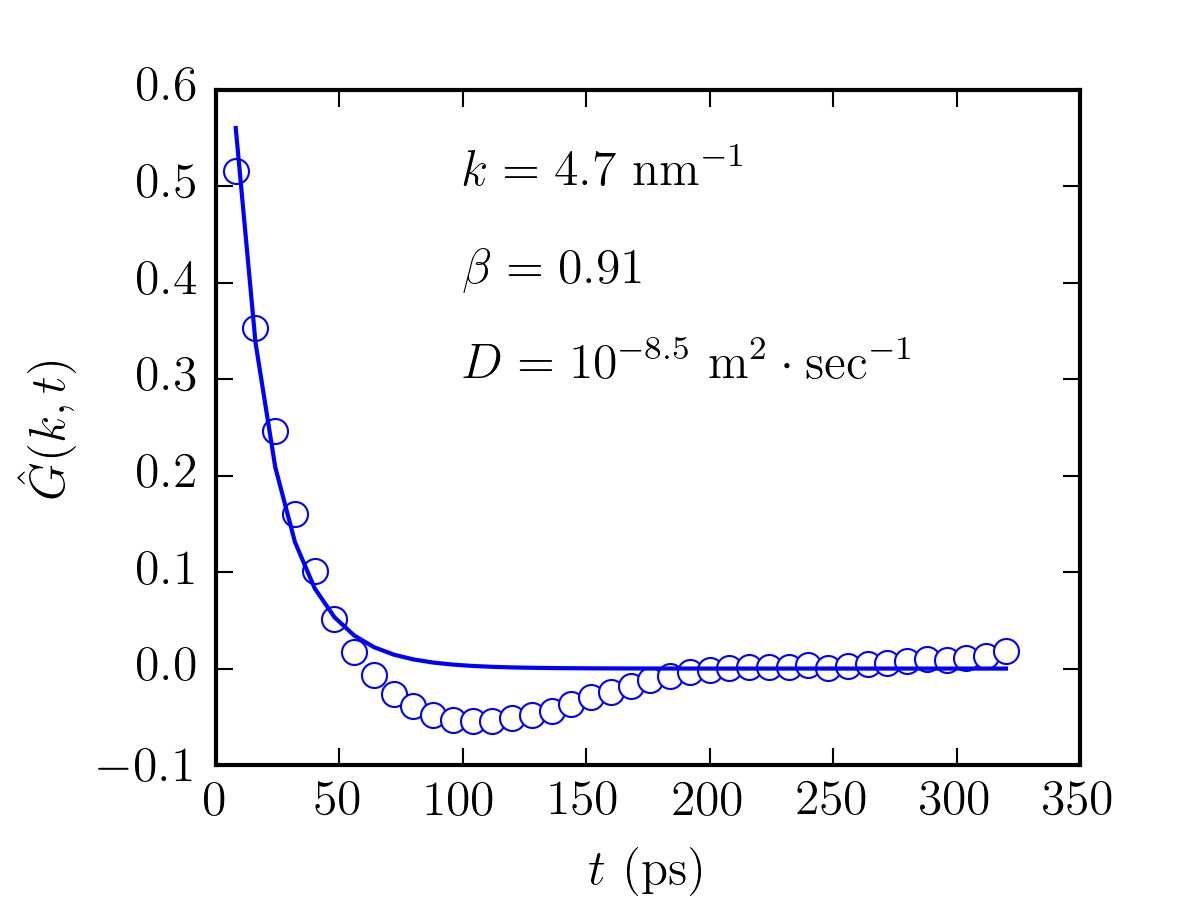
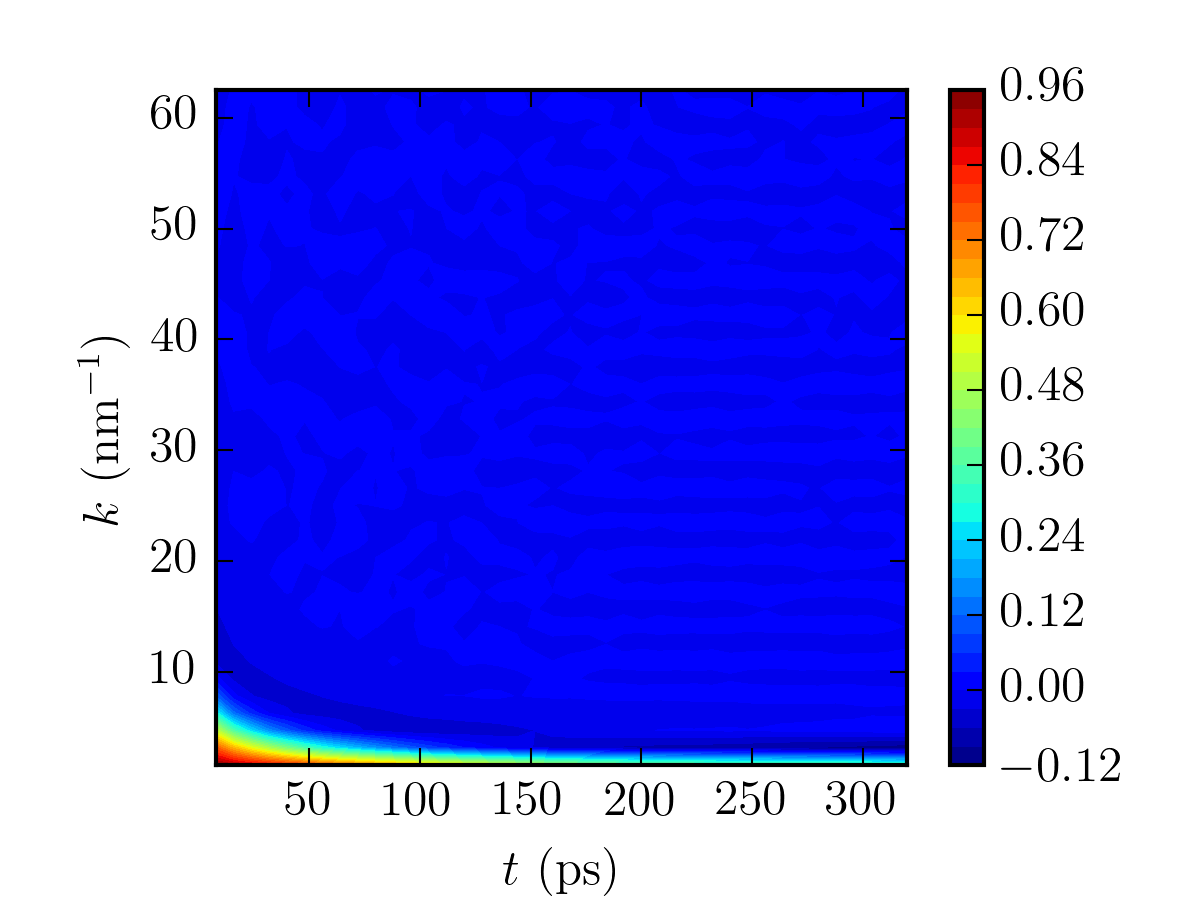
A contour plot and a 3D plot are generated as belows. Again, for benzene rings, as $k$ is small, it takes a longer time for the structure factor to decay to zero, and vice and versa for larger value of $k$. The 3D plot also makes this more obvious. At $k=4.7~\mathrm{nm^{-1}}$, $\hat{G}(k,t)$ is fitted to a stretched exponential function with the following form: \begin{equation} \exp\Big[-(k^2Dt)^{\beta}\Big] \end{equation} where $\beta$ is an indication of the non-linearity of the system, i.e. the lower the value of $\beta$, the higher the non-linearity of the system. In this case, it was found that $\beta=0.91$ and $D=10^{-8.5}~\mathrm{m^2\cdot sec^{-1}}$. The calculated value of diffusivity in this example is in agreement with that of the experimental value, which should be around $10^{-8.6}~\mathrm{m^2\cdot sec^{-1}}$ at $300$K. To reiterate, the dynamic structure factor, which is expressed as $\hat{G}(k,t)=\hat{S}(k,t)=\hat{\omega}(k,t)+\rho\hat{h}(k,t)$, consists of the intramolecular ($\hat{\omega}(k,t)$) and intermolecular ($\hat{h}(k,t)$) part.