Let us start with a vector $\mathbf{l_1}$ with a length of $l$ so that it can be explicitly written as: \begin{equation} \mathbf{l_1}=\begin{bmatrix} l\\ 0 \\ 0\\ \end{bmatrix} \end{equation} This vector $\mathbf{l_1}$ can be considered as a bond between two atoms. Say if we would like to construct a triatomic molecule, such as water. Then, there shall be two bonds. And the second bond shall form a bond angle $\theta$ with the first bond. The coordinates for the second bond vector $\mathbf{l_2}$ can be generated with the knowledge of a rotation matrix as well as $\mathbf{l_1}$. The rotation matrix is expressed as follows: \begin{equation} \mathbf{T_1}=\begin{bmatrix} \cos\theta & \sin\theta & 0\\ \sin\theta & -\cos\theta & 0\\ 0 & 0 & -1\\ \end{bmatrix} \end{equation} So that: \begin{equation} \mathbf{l_2}=\mathbf{T_1l_1}=\begin{bmatrix} \cos\theta & \sin\theta & 0\\ \sin\theta & -\cos\theta & 0\\ 0 & 0 & -1\\ \end{bmatrix}\begin{bmatrix} l \\ 0 \\ 0 \\ \end{bmatrix}=\begin{bmatrix} l\cos\theta\\ l\sin\theta \\ 0 \\ \end{bmatrix} \end{equation} The coordinates of the $i$th atom of the molecule can be calculated: \begin{equation} \mathbf{r_i}=\sum_{j=1}^{i}\mathbf{l_j}~~~(\mathrm{for~}i\geq 1) \end{equation} And $\mathbf{r_0}=\begin{bmatrix} 0 & 0 & 0 \end{bmatrix}^T$. With these, we can immediately write the .xyz file for this simple triatomic molecule (note that .xyz file can easily be read by Avogadro software)

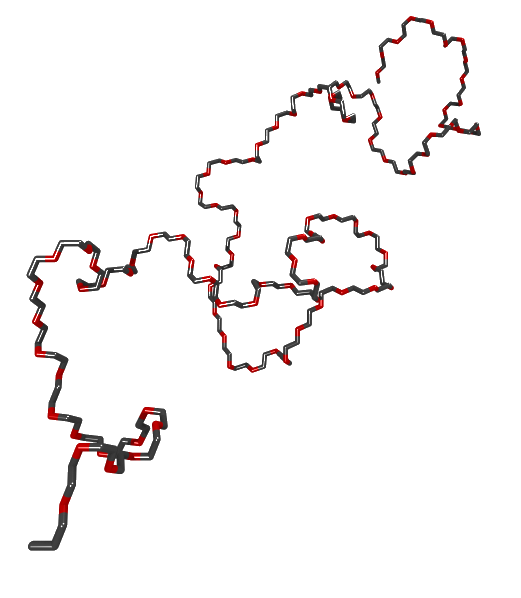
The case of triatomic molecule is extremely simple due to the absence of torsional angle. We have assumed the bond length $l=1.54~\mathrm{angstroms}$ and bond angle $\theta=68^{\circ}$. If the number of atoms exceeds three, we will then have to consider the following rotation matrix: \begin{equation} \mathbf{T_i}=\begin{bmatrix} \cos\theta & \sin\theta & 0 \\ -\sin\theta\cos\phi & \cos\theta\cos\phi & -\sin\phi\\ -\sin\theta\sin\phi & \cos\theta\sin\phi & \cos\phi\\ \end{bmatrix},~~~(\mathrm{for}~i>1) \end{equation} The angle $\phi$ is the torsional angle, which is formed by the four atoms. The third bond in global coordinate can then be explicitly written as: \begin{align} \mathbf{l_3}=\mathbf{T_1}\mathbf{T_2}\mathbf{l_1}&=\begin{bmatrix} \cos\theta & \sin\theta & 0\\ \sin\theta & -\cos\theta & 0\\ 0 & 0 & 1\end{bmatrix}\begin{bmatrix} \cos\theta & \sin\theta & 0 \\ -\sin\theta\cos\phi & \cos\theta\cos\phi & -\sin\phi\\ -\sin\theta\sin\phi & \cos\theta\sin\phi & \cos\phi\\ \end{bmatrix}\begin{bmatrix} l \\ 0 \\ 0 \\ \end{bmatrix}\\ &=\begin{bmatrix} \cos\theta & \sin\theta & 0\\ \sin\theta & -\cos\theta & 0\\ 0 & 0 & 1\end{bmatrix}\begin{bmatrix} l\cos\theta \\ -l\sin\theta\cos\phi \\ -l\sin\theta\sin\phi \\ \end{bmatrix}\\ &=\begin{bmatrix} l\cos^2\theta-l\sin^2\theta\cos\phi\\ l\sin\theta\cos\theta+l\sin\theta\cos\theta\cos\phi \\ -l\sin\theta\sin\phi\\ \end{bmatrix} \end{align} The coordinate of the fourth atom can then be calculated as: \begin{equation} \mathbf{r_3}=\sum_{j=1}^3\mathbf{l_j}=\mathbf{l_1}+\mathbf{T_1l_1}+\mathbf{T_1T_2l_1} \end{equation} Such calculation can be easily implemented for a molecule with $n$ constituent atoms. This can be done with any programming language you like. In this document, the calculation was done in python 3. A $trans$ conformation corresponds to a torsion angle $\phi=0^{\circ}$, whereas a $gauche$ conformation corresponds to a torsion angle of either $\phi=300^{\circ}$ or $\phi=60^{\circ}$. Say, the statistical weight for a trans conformation is 1, and that for gauche conformation is $\sigma$. If we consider the interdependence of the $trans$ and $gauche$ conformation, we can then figure out the statistical weight of a $trans-gauche$ ($tg$) conformation is therefore $2\sigma$. The prefactor of 2 indicates that there are two different torsional angles corresponding to the gauche state (either $\phi=300^{\circ}~(g^{+})$ or $\phi=60^{\circ}~(g^{-})$). Note that the statistical weight for $g^+g^-$ is $\sigma^2\omega$. The additional factor of $\omega$ shows that there is an extra energy penalty for such second-order interaction. The exact values of $\sigma$ as well as $\omega$ are trivial as long as they are less than one, and $\omega$ is greater than $\sigma$. This is because during the equilibriation runs of the MD simulation, the polymer chain shall relax to the equilibrium state. Figure 1 shows the configuration of a PEO chain with 100 repeat units generated according to the torsional angles assigned by the interdependence model.

A brief introduction and software can be found in this video.